Идея о том, что пространство и время взаимосвязаны, не нова. Наверняка читатель с ней знаком. Я же призываю читателя не искать связь между пространством и временем, а постараться понять, что это одно и тоже. В этой части вам не надо задумываться, где пространство, где время, где движение, а где покой. Постарайтесь просто принять пространство-время, как единое поле, имеющее некоторые экзотические свойства.
Мы будем рассматривать двухмерное представление пространства-времени, но выберем более удобные единицы. Давайте условимся, что по оси y мы будем откладывать время в секундах, а по оси x за единицу примем расстояние, которое свет проходит за секунду или просто c·1c. Чтобы пересчитать обычное расстояние (выраженное в метрах) в наши единицы, следует поделить его на скорость света (x/c).
На этом я хочу временно прервать обсуждение того, как пространство-время связано с нашим пониманием пространства и времени. Не придавайте пока большого значения этой связи. Давайте рассмотрим пространство-время не предвзято, не пытаясь найти ему аналогии в нашем мире.
Как измеряется расстояние в пространстве-времени?
Обратите внимание, мы будем измерять не расстояние в нашем обычном понимании и не время, а именно расстояние в пространстве-времени, называемое интервалом.
Оказывается, квадрат интервала равен разности:
Это выражение очень похоже на выражение для обычной длины отрезка в Евклидовой геометрии (в нашем обычном пространстве), но вместо знака «+» в нём фигурирует «-».
Справедливости ради следует сказать, что в полном четырёхмерном пространстве-времени, и при измерении величин в привычных единицах (метрах и секундах), интервал выражается формулой:
Как видите, благодаря тому, что за единицу измерения расстояния мы приняли не метр, а «расстояние, которое свет проходит за секунду», мы «избавились» от скорости света в знаменателе.
Часто используются другие выражения для интервала, которые, впрочем, не меняют его смысл. Например:
Первое, что бросается в глаза, это то, что квадрат интервала может быть и положительным и отрицательным. В зависимости от этого интервалы разделяют на пространственноподобные и времениподобные (смысл этих названий мы обсудим далее).
Кроме того, для любой точки существует бесконечно много точек, расстояние до которых равно нулю. Действительно, если мы возьмём, для примера, две точки с координатами (0, 0) и (1, 1) и вычислим интервал между ними, то получим 0.
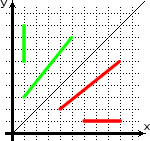
Все эти факты отражены на рисунке:

Здесь зелёным показаны времениподобные интервалы, красным — пространственноподобные, тонкая диагональная линия, идущая под углом 45 градусов, это точки, находящиеся на расстоянии 0 от центра координат (дальше мы ещё столкнёмся с ними, как с точками, лежащими на «световом конусе»).
Как видите (и как следует из формулы для интервала), если наклон отрезка меньше 45 градусов, то отрезок пространственоподобен, если же угол больше, то — времениподобен.
Из-за того, что мы вычисляем интервал необычным образом, равными могут оказаться отрезки, которые на наш взгляд не равны. На рисунке, приведённом выше, зелёные отрезки равны друг другу (для «короткого» s2=32-02=9; для «длинного» s2=52-42=9). Красные тоже равны друг другу (для обоих s2=-9).
Как привыкнуть к такой странной геометрии?
На самом деле мы постоянно сталкиваемся с не-евклидовыми геометриями.
Представьте, что вы стоите на бесконечной клетчатой плоскости. Границы клеток образуют параллельные прямые, но если вы посмотрите на горизонт, то увидите, что все эти прямые сходятся в одной точке. За вашей спиной они сходятся в другой точке. Таким образом с вашей точки зрения параллельные прямые будут пересекаться.
Если у вас есть аквариум, то вы можете проделать другой эксперимент: приблизьте лицо вплотную к стеклу и посмотрите на заднюю стенку. Она покажется вам выпуклой. С вашей точки зрения сумма углов треугольника, нарисованного на той стенке не будет равна 180 градусам.
Представьте, что пространство-время кажется нам странным только потому, что мы смотрим на него через некую призму.