
О фракталах говорят много. В Паутине созданы сотни сайтов, посвящённых фракталам. Но большая часть информации сводится к тому, что фракталы это красиво. Загадочность фракталов объясняют их дробной размерностью, но мало кто понимает, что же такое дробная размерность.
Где-то в 1996 меня заинтересовало, что же такое дробная размерность и каков её смысл. Каково же было моё удивление, когда я узнал, что это не такая уж сложная вещь, и понять её может любой школьник.
Я постараюсь изложить здесь популярно, что же такое дробная размерность. Чтобы компенсировать острый дефицит информации по этой теме.
Сперва небольшое введение, чтобы привести наши бытовые представления об измерении тел в некоторый порядок.
Не стремясь к математической точности формулировок, давайте разберёмся, что же такое размер, мера и размерность.
Размер объекта можно померить линейкой. В большинстве случаев размер получается малоинформативен. Какая «гора» больше?

Если сравнивать высоты, то больше красная, если ширины — зелёная.
Сравнение размеров может быть информативным если предметы подобны друг другу:

Теперь какие бы размеры мы ни сравнили: ширину, высоту, сторону, периметр, радиус вписанной окружности или любые другие, всегда получится, что зелёная гора больше.
Далее мы будем говорить о подобных объектах, поэтому размер нам пригодится.
Мера тоже служит для измерения объектов, но она измеряется не линейкой. О том, как именно она измеряется мы ещё поговорим, а пока отметим её главное свойство — мера аддитивна.
Выражаясь на бытовом языке, при слиянии двух объектов, мера суммы объектов равна сумме мер исходных объектов.
Для одномерных объектов мера пропорциональна размеру. Если вы возьмёте отрезки длиной 1см и 3см, «сложите» их вместе, то «суммарный» отрезок будет иметь длину 4см (1+3=4см).
Для не одномерных тел, мера вычисляется по некоторым правилам, которые подбираются так, чтобы мера сохраняла аддитивность. Например, если вы возьмёте квадраты со сторонами 3см и 4см и «сложите» их (сольёте их вместе), то сложатся площади (9+16=25см²), то есть сторона (размер) результата будет 5см.
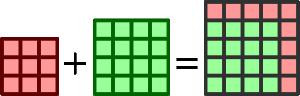
И слагаемые, и сумма являются квадратами. Они подобны друг другу и мы можем сравнивать их размеры. Оказывается, что размер суммы не равен сумме размеров слагаемых (5≄4+3).
Как же связаны мера и размер?
Как раз размерность и позволяет связать меру и размер.
Давайте обозначим размерность — D, меру — M, размер — L. Тогда формула, связывающая эти три величины будет имеют вид:
Для привычных нам мер эта формула приобретает всем знакомые обличия. Для двухмерных тел (D=2) мерой (M) является площадь (S), для трёхмерных тел (D=3) — объём (V):
Внимательный читатель спросит, по какому праву мы написали знак равенства? Ну хорошо, площадь квадрата равна квадрату его стороны, а площадь круга? Работает ли эта формула для любых объектов?
И да и нет. Вы можете заменить равенства на пропорциональности и ввести коэффициенты, а можете считать, что мы вводим размеры тел именно так, чтобы формула работала. Например для круга мы будем называть размером длину дуги равной корень из «пи» радиан. А почему нет?
В любом случае, наличие или отсутствие коэффициентов не изменит суть дальнейших рассуждений. Для простоты, я не буду вводить коэффициенты; если хотите, вы можете их добавить самостоятельно, повторить все рассуждения и убедиться, что они (рассуждения) не утратили своей справедливости.
Из всего сказанного нам следует сделать один вывод, что если фигуру уменьшить в N раз (отмасштабировать), то она будет укладываться в исходной ND раз.
Действительно, если уменьшить отрезок (D=1) в 5 раз, то он поместится в исходном ровно пять раз (51=5); Если треугольник (D=2) уменьшить в 3 раза, то он уложится в исходном 9 раз (32=9).
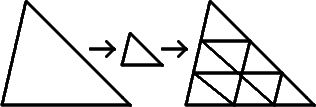
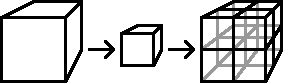
Если куб (D=3) уменьшить в 2 раза, то он уложится в исходном 8 раз (23=8).
Верно и обратное: если при уменьшении размера фигуры в N раз, оказалось, что она укладывается в исходной n раз (то есть мера её уменьшилась в n раз), то размерность можно вычислить по формуле:
Не очень строго и опуская многие важные детали, мы всё же получили формулу для размерности.
Про дробную размерность обычно рассказывают на примерах различных ломаных. Я не буду изобретать велосипед и обращусь к звезде Коха.
Процедура её построения показана на рисунке (снизу вверх):
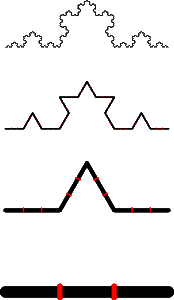
В начале берётся отрезок, делится на три равные части и средняя часть заменяется на два отрезка, равных изъятому. Получается ломаная из четырёх равных отрезков.
На втором шаге действия повторятся с каждым из четырёх отрезков и получается ломаная из 16 отрезков.
Эти построения повторяются бесконечное число раз и в конце концов у нас получается ломаная, состоящая из бесконечного числа отрезков. Сколько бы мы её не масштабировали, мы всё равно будем получать одно и тоже.

Это и есть звезда Коха.
Строго говоря, полученное множество точек уже нельзя называть ломаной. По определению, ломаная должна состоять из конечного числа отрезков. Но я буду использовать слово «ломаная» в «нестрогом» смысле для краткости.
Давайте теперь воспользуемся нашим приёмом, чтобы определить её размерность.
Из построения и рисунка видно, что звезду можно разбить на четыре равные части, при этом размер (скажем, длина исходного отрезка) каждой части будет равен трети размера исходной фигуры. То есть будучи уменьшена в три раза, она уложится в себе четыре раза:
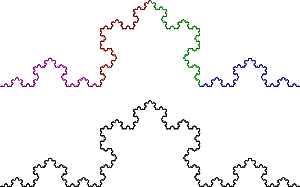
По аналогии с нашими предыдущими рассуждениями получаем, что размерность равна
То есть это уже не просто отрезок или ломаная (длина звезды Коха бесконечна), но и не плоская фигура, полностью покрывающая некоторую площадь.
Если мы слегка модифицируем алгоритм построения и будем извлекать не 1/3 отрезка, а 1/9, то ломаная получится более плотной:

Какова же её размерность? Теперь фигура уложится сама в себе четыре раза после уменьшения в 9/4 раза, то есть размерность можно вычислить по той же формуле:
Как видите, «плотность» покрытия сразу отразилась на размерности.
Давайте теперь получим более общую формулу для вычисления размерности. Для этого снова рассмотрим пример:

Итерации снова начинаются с одного отрезка. На каждом шаге итерации количество отрезков удваивается. Каждый порождает два новых: один в 0.88 раз меньше (или, вернее больше) родителя, второй — в 0.41 раз. В пределе получается следующее множество:
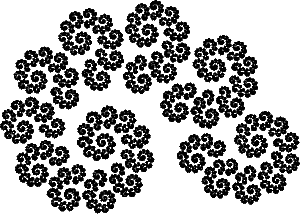
Давайте вернёмся к первому шагу итераций, на котором мы получили два отрезка, и посмотрим, какая часть фрактала образована из каждого из них:

Если принять, что размер полного фрактала 1, то размер зелёной части (полученной из большего отрезка) будет 0.88, а размер красной (полученной из меньшего) — 0.41.
Та формула, которой мы располагаем, уже не годится, так как мы имеем не один, а два коэффициента масштабирования. Но мы можем воспользоваться нашими знаниями о свойства меры, размера и размерности. Мера, как мы помним, аддитивна, то есть мера полного фрактала, равна сумме мер его частей:
И сам фрактал, и его части имеют одинаковую размерность (D) и мы можем выразить меры, через размеры:
А размеры мы знаем. То есть для размерности нашего фрактала мы можем написать уравнение:
или просто
Решить это уравнение аналитически невозможно, но «приблизительный» ответ можно «подобрать». В нашем случае
Можете проверить на калькуляторе.
Таким образом, если фрактал образован из N подобных элементов, с коэффициентами подобия k1, k2 ... kN, то его размерность можно найти из уравнения:
По этой формуле уже можно рассчитать размерность многих итерационных систем.
Обратите внимание, что, если все коэффициенты равны, то наша формула превращается в уже известную простую формулу:
или
Последнее выражение есть наша первая простая формула для вычисления размерности простейших самоподобных фракталов.
В этом рассказе (именно рассказе) о размерности даже не упомянуты многие важные аспекты. Он ни сколько не претендует на полноту, точность или строгость. Но, надеюсь, что он будет понятен любому старшекласснику и развеет многие непонимания и мистификации. Про одну из таких распространённых мистификаций вы можете прочитать в моей следующей заметке.
комментарии (экспериментальная возможность)