Построение гипотез по методу наименьших квадратов — это, пожалуй, простейшая и наиболее распространённая задача машинного обучения и построения прогнозов.
Здесь я приведу полезные и наиболее употребительные сниппеты для Python. Однако, я хотел бы сделать эту заметку чуть-чуть более полезной, что просто сниппет. Предлагаю решить практическую задачу.
Я написал расширение для браузера Chrome, позволяющее слушать радио. Я слежу за статистикой установок и имею данные по количеству пользователей. Накопив определённую статистику, я хочу получить ответы на два простых вопроса:
Чтобы решить эту задачу нам нужна модель. Давайте исходить из того, что зависимость числа пользователей от дня — полиномиальная.
Переберём пять гипотез:
Вот код:
#!/usr/bin/python
# coding: utf8
import scipy as sp
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
# читаем данные
data = sp.genfromtxt("data.tsv", delimiter="\t")
#print(data[:10]) # часть данных можно напечатать, чтобы убедиться, что всё в порядке
# берём срезы: первую и вторую колонку нашего файла
x = data[:,0]
y = data[:,1]
# настраиваем детали отрисовки графиков
plt.figure(figsize=(8, 6))
plt.title("Installations")
plt.xlabel("Days")
plt.ylabel("Installations")
#plt.xticks([...], [...]) # можно назначить свои тики
plt.autoscale(tight=True)
# рисуем исходные точки
plt.scatter(x, y)
legend = []
# аргументы для построения графиков моделей: исходный интервал + 60 дней
fx = sp.linspace(x[0], x[-1] + 60, 1000)
for d in range(1, 6):
# получаем параметры модели для полинома степени d
fp, residuals, rank, sv, rcond = sp.polyfit(x, y, d, full=True)
#print("Параметры модели: %s" % fp1)
# функция-полином, если её напечатать, то увидите математическое выражение
f = sp.poly1d(fp)
#print(f)
# рисуем график модельной функции
plt.plot(fx, f(fx), linewidth=2)
legend.append("d=%i" % f.order)
f2 = f - 1000 # из полинома можно вычитать
t = fsolve(f2, x[-1]) # ищем решение уравнения f2(x)=0, отплясывая от точки x[-1]
print "Полином %d-й степени:" % f.order
print "- Мы достигнем 1000 установок через %d дней" % (t[0] - x[-1])
print "- Через 60 дней у нас будет %d установок" % f(x[-1] + 60)
plt.legend(legend, loc="upper left")
plt.grid()
plt.savefig('data.png', dpi=50)
plt.show()
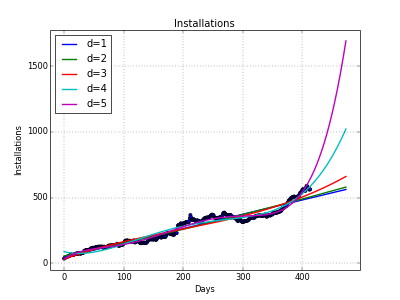
А вот результат:
Полином 1-й степени:
- Мы достигнем 1000 установок через 462 дней
- Через 60 дней у нас будет 561 установок
Полином 2-й степени:
- Мы достигнем 1000 установок через 368 дней
- Через 60 дней у нас будет 579 установок
Полином 3-й степени:
- Мы достигнем 1000 установок через 166 дней
- Через 60 дней у нас будет 660 установок
Полином 4-й степени:
- Мы достигнем 1000 установок через 57 дней
- Через 60 дней у нас будет 1021 установок
Полином 5-й степени:
- Мы достигнем 1000 установок через 28 дней
- Через 60 дней у нас будет 1692 установок
Мы так же можем взглянуть на графики, построенные с помощью matplotlib.pyplot:

Здесь хорошо видны примеры и переученности (overfitting) и недоученности (underfitting). Видно, что наиболее реалистичны кривые первой и второй степени. Результаты же, полученные на кривых четвёртой и пятой степеней, скорее всего, обманчивы.